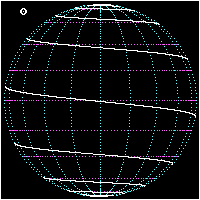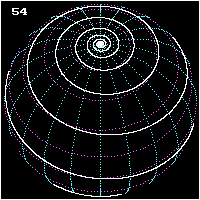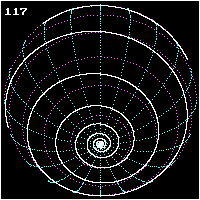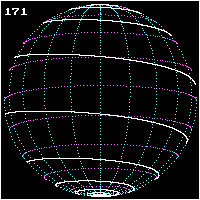
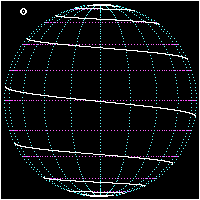
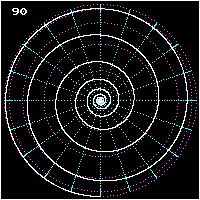
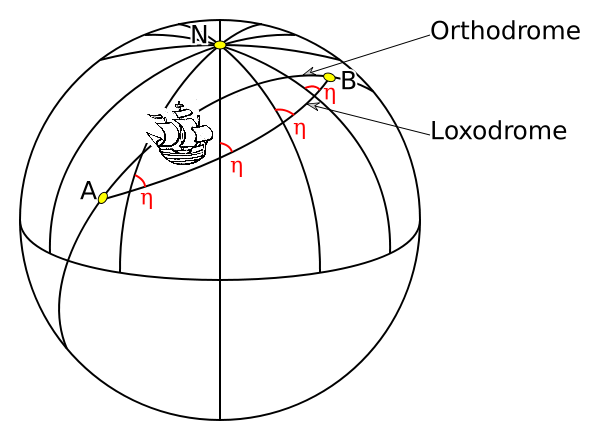
 Bernoulli zeigte als erstes, dass alle Spiralradien mit der zu ihnen gehörenden Spiralentangente einen gleich großen Winkel bilden. Wegen dieser Eigenschaft nannte er diese Art Kurven Loxodromen (wörtlich übersetzt: schief Laufende!). Wir gewinnen eine Vorstellung von einer solchen Linie, wenn wir uns ein Schiff fahrend denken, das seinen Kurswinkel gegen die Nordrichtung während der Fahrt beibehält, etwa immer genau nach Nordosten fährt wie in der Figur links dargestellt.
Es wird dann den Nordpol in unzähligen, unfassbar eng werdenden Windungen umkreisen müssen. Die Fahrlinie liegt allerdings dann auf einer Kugeloberfläche und wird sphärische Loxodrome genannt.
Früher wurde in der See- und Luftfahrt oft mit dem Kompass navigiert. Es war günstig, entlang einer Loxodrome zu reisen, da man dann immer nur einer Peilung (Kompassrichtung) folgen musste. Zwar ist die Strecke der Loxodrome immer länger als die der Orthodrome (nur wenn die Loxodrome auf einem Großkreis liegt, können sie gleich lang sein) – dafür muss man aber nicht ständig einen neuen Kurswinkel berechnen.
Bernoulli zeigte als erstes, dass alle Spiralradien mit der zu ihnen gehörenden Spiralentangente einen gleich großen Winkel bilden. Wegen dieser Eigenschaft nannte er diese Art Kurven Loxodromen (wörtlich übersetzt: schief Laufende!). Wir gewinnen eine Vorstellung von einer solchen Linie, wenn wir uns ein Schiff fahrend denken, das seinen Kurswinkel gegen die Nordrichtung während der Fahrt beibehält, etwa immer genau nach Nordosten fährt wie in der Figur links dargestellt.
Es wird dann den Nordpol in unzähligen, unfassbar eng werdenden Windungen umkreisen müssen. Die Fahrlinie liegt allerdings dann auf einer Kugeloberfläche und wird sphärische Loxodrome genannt.
Früher wurde in der See- und Luftfahrt oft mit dem Kompass navigiert. Es war günstig, entlang einer Loxodrome zu reisen, da man dann immer nur einer Peilung (Kompassrichtung) folgen musste. Zwar ist die Strecke der Loxodrome immer länger als die der Orthodrome (nur wenn die Loxodrome auf einem Großkreis liegt, können sie gleich lang sein) – dafür muss man aber nicht ständig einen neuen Kurswinkel berechnen.
 Auf kürzeren Strecken ist die Navigation auf der Loxodrome nur unwesentlich länger als die Navigation auf der Orthodrome. Auf längeren Strecken macht sich der Unterschied zwischen Ortho- und Loxodrome jedoch deutlich bemerkbar, wie das Bild rechts zeigt.
Auf kürzeren Strecken ist die Navigation auf der Loxodrome nur unwesentlich länger als die Navigation auf der Orthodrome. Auf längeren Strecken macht sich der Unterschied zwischen Ortho- und Loxodrome jedoch deutlich bemerkbar, wie das Bild rechts zeigt.Im karthesischen Koordinatensystem und mit dem Kugelradius r liest sich die Loxodrome in Parametersarstellung wie folgt:
| x | = | r⋅cos λ cosh(k λ) |
||
| y | = | r⋅sin λ cosh(k λ) |
||
| z | = | r⋅tanh(k λ) |
mit λ dem Längengrad und k = cot η, der Steigung des Reiseverlaufes.
Da der Gunter vorwiegend in der Seefahrt praktischen Nutzen fand, sollte somit verständlich sein, warum viele Exemplare eine Loxodromen-Skala aufwiesen.